I like well-made things. Software is not an exclusion. And what I do myself is not exclusion either, so when I decided to opt in to Fallout™ original games' remakes, I knew: it would be a challenge — not only because of me being newcomer to game development, but because of pretty vague information about how the games actually work too.
While it has been done a lot by a community after all these years, some things still seem not so clear. Today we will talk about tiles' geometry in original Fallout™ games, and how I managed to get rid from as much of a hardcode, as it was possible.
Original Fallout's BIS Mapper
Back in the day there was a tool released by a publisher of original games — Mapper 2. It was among others used by the developers in the company. As the games itself, it was buggy, and since it wasn't supposed to be released to public at any point of time, it was buggy a lot. Nonetheless, it has always been the way to edit maps for both games. I saw some attempts to implement new software for this purpose, but wasn't able to acquire something working. Any modern code now have some ported values, hardcoded in the original Mapper.
It seems to me, no one have figured out, what that hardcode really means, or, at least, no one bothered enough to eliminate it from modern codebases. Well... it bothers me.
What we know
Tiles in Fallout™ use 100-sized grid, while all other objects use 200-sized grid, since they lie in hexagonal grid: 4 hexes per 1 tile. In this thread, someone suggests this code for converting coordinates from tiles' to screen's:
var sx = 4752 + (32 * y) - (48 * x)
var sy = (24 * y) + (12 * x)
What this does even mean? Why is it so heavily driven by hardcode numbers? Does it relate to screen resolution somehow, or edge cases, or what? May be it’s better to check out some modern code, like in here? Some guy started to reimplement Fallout™ 2 in Rust — very similar to my goal! Let’s take a look...
pub fn to_screen(p: Point) -> Point {
let screen_x = 48 * p.x + 32 * p.y;
let screen_y = -12 * p.x + 24 * p.y;
Point::new(screen_x, screen_y)
}
Okay, it seems, he got rid of some screen constants, but these magic 48, 32, 24 and 12 still here. At this point I realised, that it’s just simpler and better to investigate it myself.
Digging in
To start with, I watched this talk by Tim Cain one more time. He’s speaking in there about cavalier oblique projection used in Fallout™ games, because it’s common to think that the games were isometric. They weren’t. There’s nice guide to tiles’ math when the projection is isometric, which shows, how tiles are shifted relative to each other. Luckily, when the projection is isometric, you got these sugar coefficients, like 1/2 of tile’s width and height. For projection used in Fallout™, we need to do a little math here. Let’s start with scheme and known values.
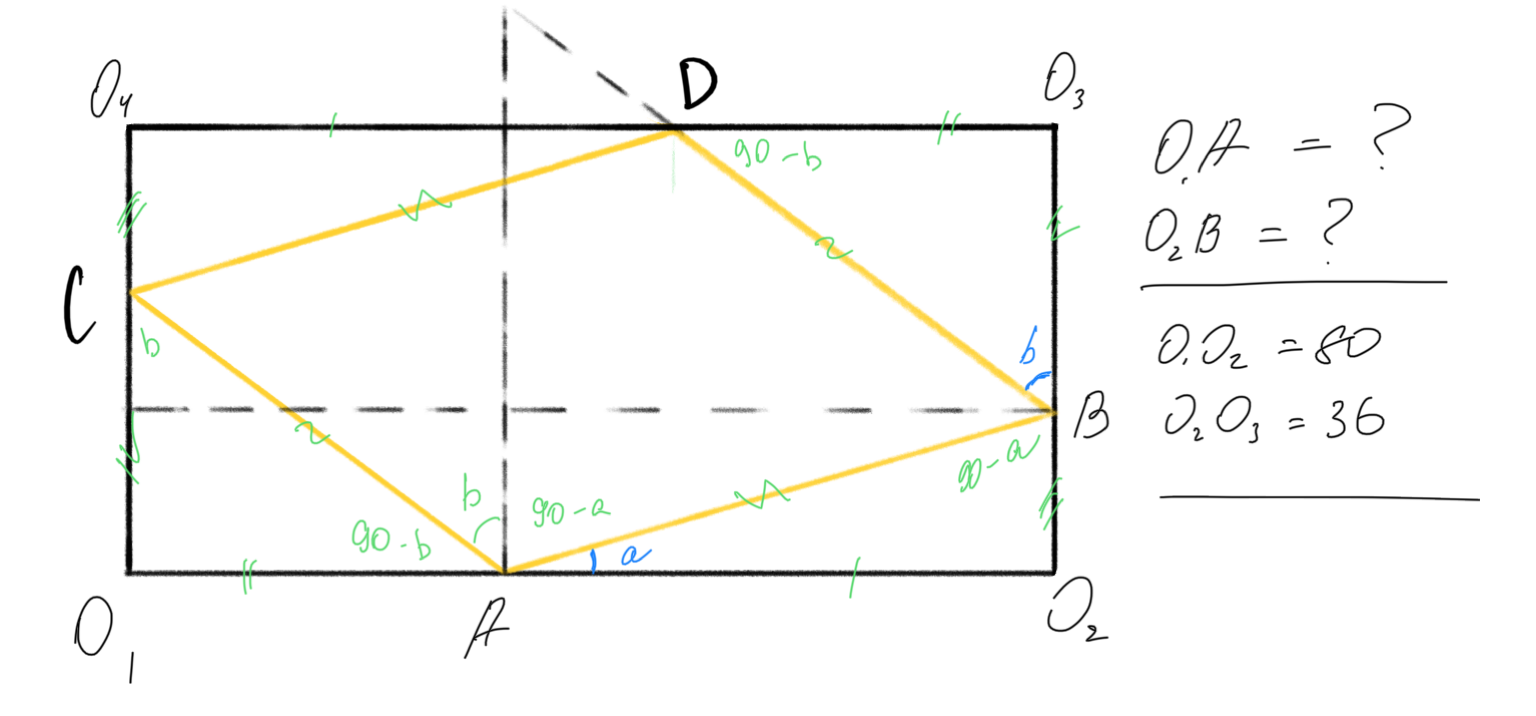
Tiles must be placed in such a way, that each AB side of one’s is a CD side of the others, as well as AC side is someone’s BD side. It looks like this; refer to square grid indexing to understand, what’s going on here:
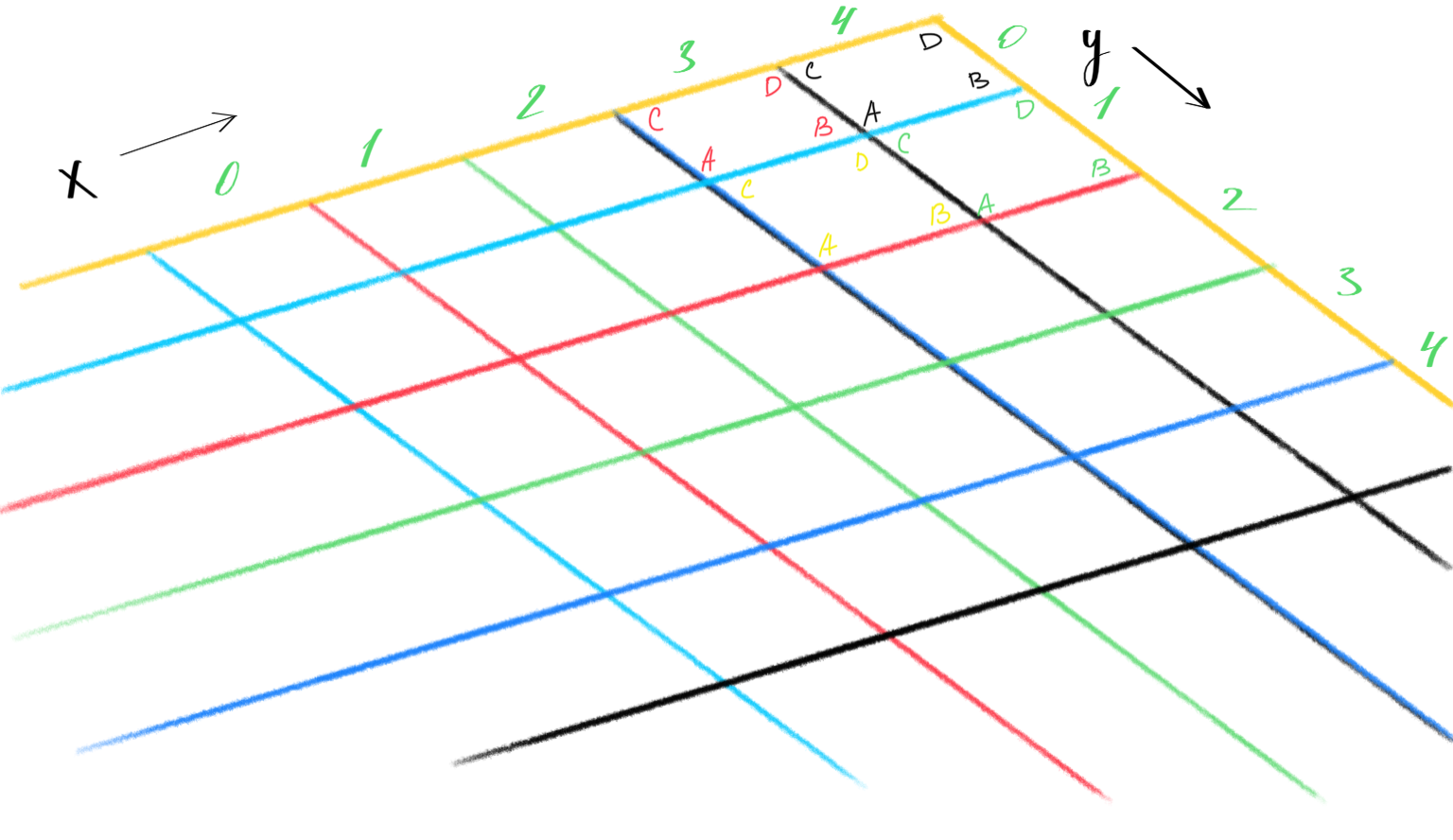
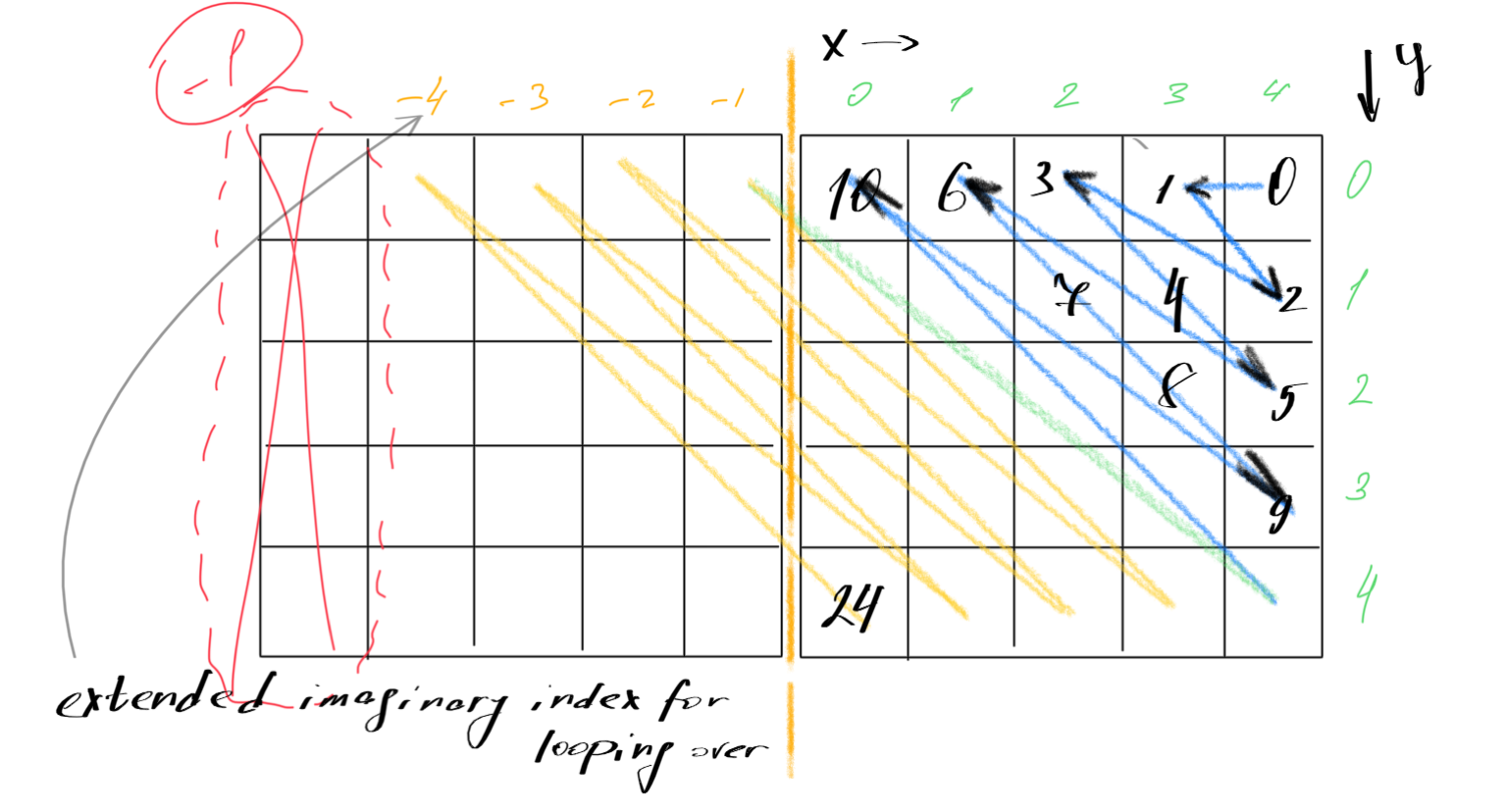
Also, we render tiles from back to front, so to begin with coordinates’ rendering, we have the following:
Calculating Coefficients
Given tiles’ dimensions and assuming they are all equal, we must have a way to calculate shifts, needed to adjust positions for each tile’s coordinate. Those shifts seem to be O1A for horizontal axis and O2B for vertical one. Which are equal to O3D and O4C respectively.
Fallout™ uses tiles with width of 80 and heigh of 36. Those are values I’d like to be variable to support in my code, as long as the angles of projection remain the same. This will allow to use bigger tiles in my engine with same projections angles, since modern machines work better with bigger chunks of data, due to rising ubiquity of SSD’s and for number of other reasons.
For the width this must be true:
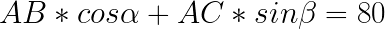
And for the height:
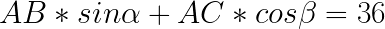
Thus leading us to following linear equations’ system:
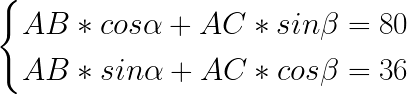
Rearranging sides, knowing which are equal, gives us another system, which involves lengths we are looking for:
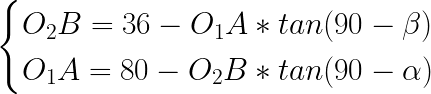
But wait, we don’t know the angles! Here’s 4 variables in two-members system, so we need to eliminate 2 others, and we actually can: from those hardcoded values in others’ code! They’re just shifts, which we are trying to find formula for, pre-calculated for Fallout™ tiles’ width and height. So, putting them into this system (O2B and O1A), we’re getting our angles:
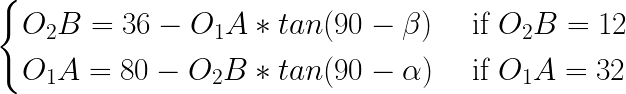
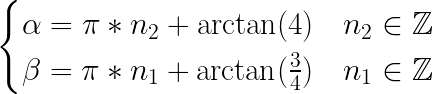
Which gives us values for angles: arctan(3/4) ~= 36.87º and arctan(4) ~= 75.96º. Note, that those are just the angles of projected image, not the projection itself. With known angles, we can easily find horizontal and vertical shifts for any tile:
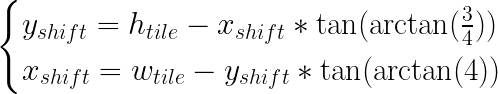
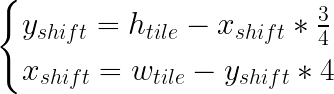
which, applied to our initial width and height of original Fallout™ tiles, yields horizontal shift equal to 32 and vertical one equal to 12:
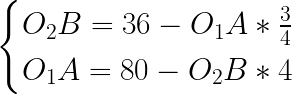
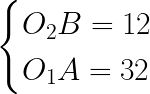
Exactly what the others used to hardcode in the engine.

